Why spatial hashing?
How often have you bemoaned the lack of a simple way to cut down on the number of objects tested during collision detection or culling? Sure, one could integrate a full-blown physics library, or implement a dynamic quad-tree/kd-tree/BVH, but all of these are time consuming, and not necessarily worth it for a small game or demo. These approaches also all suffer from another drawback (which may or may not affect you, depending on the type of game): they assume the world is a fixed, finite size.
Spatial hashing, on the other hand, is lightweight, trivial to implement, and can easily deal with worlds whose dimensions vary over time.
Why another article on spatial hashing?
There are quite a number of articles on spatial hashing floating around the net, ranging all the way from lengthy academic treatises to back of the napkin sketches. Unfortunately, most of the articles towards the beginning of that spectrum aren't that friendly to the casual observer, and towards the end of the spectrum they don't tend to provide complete implementations, or neglect the more obscure (and useful) tricks.
What is a spatial hash?
A spatial hash is a 2 or 3 dimensional extension of the hash table, which should be familiar to you from the standard library or algorithms book/course of your choice. Of course, as with most such things, there is a twist...
The basic idea of a hash table is that you take a piece of data (the 'key'), run it through some function (the 'hash function') to produce a new value (the 'hash'), and then use the hash as an index into a set of slots ('buckets').
To store an object in a hash table, you run the key through the hash function, and store the object in the bucket referenced by the hash. To find an object, you run the key through the hash function, and look in the bucket referenced by the hash.
Typically the keys to a hash table would be strings, but in a spatial hash we use 2 or 3 dimensional points as the keys. And here is where the twist comes in: for a normal hash table, a good hash function distributes keys as evenly as possible across the available buckets, in an effort to keep lookup time short. The result of this is that keys which are very close (lexicographically speaking) to each other, are likely to end up in distant buckets. But in a spatial hash we are dealing with locations in space, and locality is very important to us (especially for collision detection), so our hash function will not change the distribution of the inputs.
What is this crazy pseudo-code you are using?
That is Python. If you haven't encountered Python before, or don't favour it for some reason, then it makes fairly readable pseudo-code all by itself. Even if you have a passing familiarity with Python, however, be careful of some of the container manipulation used herein.
Where do we start?
The first thing we need to do is create the spatial hash. Because I want to deal with environments of any dimension, we are going to create what I call a 'sparse' spatial hash, and this takes a single parameter: the cell/bucket size. If we were dealing with an environment of fixed and finite dimensions, we could implement a 'dense' spatial hash instead, where we divide the environment up into cells/buckets ahead of time, and pre-allocate those buckets. However, since we don't know the size of the environment, we will still divide the world into cells, but we won't pre-allocate any buckets. We will however allocate a dictionary (hash table/hash map in other languages) to store our buckets later.
def __init__(self, cell_size):
self.cell_size = cell_size
self.contents = {}
Our hash function is also very simple, and unlike a regular hash function, all it does is classify points into their surrounding cells. It takes a 2D point as its parameter, divides each element by the cell size, and casts it to an (int, int) tuple.
def _hash(self, point):
return int(point.x/self.cell_size), int(point.y/self.cell_size)
How does one insert objects?
There simplest keys to insert are single points. These aren't generally that useful, but the concept is straightforward, and they might be used for way-points, or similar. The procedure is extremely simple: hash the point to find the right bucket, create the bucket if it doesn't yet exist, and insert the object into the bucket. In this implementation, each bucket is a simple Python list.
def insert_object_for_point(self, point, object):
self.contents.setdefault( self._hash(point), [] ).append( object )
Of course, we also need to insert more complex shapes. Rather than deal with the intricacies of determining which bucket(s) an arbitrary shape need to hash to, we support only one other primitive: the axis-aligned bounding-box. The axis-aligned bounding-box is cheap to compute for other primitives, provides a reasonably decent fit, and is incredibly simple to hash.
The astute among you will have already noticed a few problems with inserting objects other than simple points into the spatial hash: a) the object may overlap several cells/buckets if it is near the edge of a bucket, and b) an object may actually be larger than a single bucket. The solution to these is luckily also simple: we add the object to all relevant buckets. And the bounding-box approach comes into its own, as we can just hash the min and max points, and then iterate over the affected buckets.
def insert_object_for_box(self, box, object):
# hash the minimum and maximum points
min, max = self._hash(box.min), self._hash(box.max)
# iterate over the rectangular region
for i in range(min[0], max[0]+1):
for j in range(min[1], max[1]+1):
# append to each intersecting cell
self.contents.setdefault( (i, j), [] ).append( object )
What about removing objects?
There are a number of approaches to removing objects from the hash, depending on your needs. The simplest (and the one I used in the accompanying code) is to use the key - feed the position/bounding-box back into the hash function, and remove the object from the resulting bucket(s).
If you don't know the key, you can always perform a linear search over the entire spatial hash, and remove the object wherever you find it, but this of course is not great from a performance standpoint.
And lastly, you can just clear the whole structure (by deleting all the buckets), and start fresh.
And search/retrieval?
Searching follows exactly the same procedure: feed the point into the hash function, and return the list of items in the bucket.
Of course, for this to be useful for collision detection, you also need to be able to search in a range, or in our case, a bounding-box. This once again follows the same idea as insertion and removal: hash the min and max of the bounding-box, iterate over the affected cells/buckets, and build a list of all objects encountered. There is one trick, however - this list is likely to contain (potentially a lot of) duplicates. We don't want the user to have to deal with duplicates, so you need to zap them in some way. The accompanying code does this by adding them to a set (which cannot by definition contain duplicates), and converting the set back to a list, but there are many possible approaches.
How do we tune the spatial hash?
Whenever hashed data structures are discussed, the question of tuning arises. In this sparse spatial hash, we only have a single parameter to tune, namely the cell size. This cell size can have a pronounced effect on performance - too large a cell size and too many objects will end up in the same cell, too small and objects will span too many cells.
As a (very approximate) rule of thumb, I find that the cell size should be roughly twice the size of the average-sized object in your world. However, depending on the relative scales of objects, you may need to tune differently.
What else affects performance?
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?
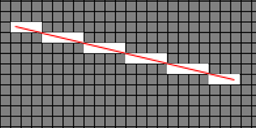
There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
There are quite a number of articles on spatial hashing floating around the net, ranging all the way from lengthy academic treatises to back of the napkin sketches. Unfortunately, most of the articles towards the beginning of that spectrum aren't that friendly to the casual observer, and towards the end of the spectrum they don't tend to provide complete implementations, or neglect the more obscure (and useful) tricks.
What is a spatial hash?
A spatial hash is a 2 or 3 dimensional extension of the hash table, which should be familiar to you from the standard library or algorithms book/course of your choice. Of course, as with most such things, there is a twist...
The basic idea of a hash table is that you take a piece of data (the 'key'), run it through some function (the 'hash function') to produce a new value (the 'hash'), and then use the hash as an index into a set of slots ('buckets').
To store an object in a hash table, you run the key through the hash function, and store the object in the bucket referenced by the hash. To find an object, you run the key through the hash function, and look in the bucket referenced by the hash.
Typically the keys to a hash table would be strings, but in a spatial hash we use 2 or 3 dimensional points as the keys. And here is where the twist comes in: for a normal hash table, a good hash function distributes keys as evenly as possible across the available buckets, in an effort to keep lookup time short. The result of this is that keys which are very close (lexicographically speaking) to each other, are likely to end up in distant buckets. But in a spatial hash we are dealing with locations in space, and locality is very important to us (especially for collision detection), so our hash function will not change the distribution of the inputs.
What is this crazy pseudo-code you are using?
That is Python. If you haven't encountered Python before, or don't favour it for some reason, then it makes fairly readable pseudo-code all by itself. Even if you have a passing familiarity with Python, however, be careful of some of the container manipulation used herein.
Where do we start?
The first thing we need to do is create the spatial hash. Because I want to deal with environments of any dimension, we are going to create what I call a 'sparse' spatial hash, and this takes a single parameter: the cell/bucket size. If we were dealing with an environment of fixed and finite dimensions, we could implement a 'dense' spatial hash instead, where we divide the environment up into cells/buckets ahead of time, and pre-allocate those buckets. However, since we don't know the size of the environment, we will still divide the world into cells, but we won't pre-allocate any buckets. We will however allocate a dictionary (hash table/hash map in other languages) to store our buckets later.
def __init__(self, cell_size):
self.cell_size = cell_size
self.contents = {}
Our hash function is also very simple, and unlike a regular hash function, all it does is classify points into their surrounding cells. It takes a 2D point as its parameter, divides each element by the cell size, and casts it to an (int, int) tuple.
def _hash(self, point):
return int(point.x/self.cell_size), int(point.y/self.cell_size)
How does one insert objects?
There simplest keys to insert are single points. These aren't generally that useful, but the concept is straightforward, and they might be used for way-points, or similar. The procedure is extremely simple: hash the point to find the right bucket, create the bucket if it doesn't yet exist, and insert the object into the bucket. In this implementation, each bucket is a simple Python list.
def insert_object_for_point(self, point, object):
self.contents.setdefault( self._hash(point), [] ).append( object )
Of course, we also need to insert more complex shapes. Rather than deal with the intricacies of determining which bucket(s) an arbitrary shape need to hash to, we support only one other primitive: the axis-aligned bounding-box. The axis-aligned bounding-box is cheap to compute for other primitives, provides a reasonably decent fit, and is incredibly simple to hash.
The astute among you will have already noticed a few problems with inserting objects other than simple points into the spatial hash: a) the object may overlap several cells/buckets if it is near the edge of a bucket, and b) an object may actually be larger than a single bucket. The solution to these is luckily also simple: we add the object to all relevant buckets. And the bounding-box approach comes into its own, as we can just hash the min and max points, and then iterate over the affected buckets.
def insert_object_for_box(self, box, object):
# hash the minimum and maximum points
min, max = self._hash(box.min), self._hash(box.max)
# iterate over the rectangular region
for i in range(min[0], max[0]+1):
for j in range(min[1], max[1]+1):
# append to each intersecting cell
self.contents.setdefault( (i, j), [] ).append( object )
What about removing objects?
There are a number of approaches to removing objects from the hash, depending on your needs. The simplest (and the one I used in the accompanying code) is to use the key - feed the position/bounding-box back into the hash function, and remove the object from the resulting bucket(s).
If you don't know the key, you can always perform a linear search over the entire spatial hash, and remove the object wherever you find it, but this of course is not great from a performance standpoint.
And lastly, you can just clear the whole structure (by deleting all the buckets), and start fresh.
And search/retrieval?
Searching follows exactly the same procedure: feed the point into the hash function, and return the list of items in the bucket.
Of course, for this to be useful for collision detection, you also need to be able to search in a range, or in our case, a bounding-box. This once again follows the same idea as insertion and removal: hash the min and max of the bounding-box, iterate over the affected cells/buckets, and build a list of all objects encountered. There is one trick, however - this list is likely to contain (potentially a lot of) duplicates. We don't want the user to have to deal with duplicates, so you need to zap them in some way. The accompanying code does this by adding them to a set (which cannot by definition contain duplicates), and converting the set back to a list, but there are many possible approaches.
How do we tune the spatial hash?
Whenever hashed data structures are discussed, the question of tuning arises. In this sparse spatial hash, we only have a single parameter to tune, namely the cell size. This cell size can have a pronounced effect on performance - too large a cell size and too many objects will end up in the same cell, too small and objects will span too many cells.
As a (very approximate) rule of thumb, I find that the cell size should be roughly twice the size of the average-sized object in your world. However, depending on the relative scales of objects, you may need to tune differently.
What else affects performance?
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?

There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
That is Python. If you haven't encountered Python before, or don't favour it for some reason, then it makes fairly readable pseudo-code all by itself. Even if you have a passing familiarity with Python, however, be careful of some of the container manipulation used herein.
Where do we start?
The first thing we need to do is create the spatial hash. Because I want to deal with environments of any dimension, we are going to create what I call a 'sparse' spatial hash, and this takes a single parameter: the cell/bucket size. If we were dealing with an environment of fixed and finite dimensions, we could implement a 'dense' spatial hash instead, where we divide the environment up into cells/buckets ahead of time, and pre-allocate those buckets. However, since we don't know the size of the environment, we will still divide the world into cells, but we won't pre-allocate any buckets. We will however allocate a dictionary (hash table/hash map in other languages) to store our buckets later.
def __init__(self, cell_size):
self.cell_size = cell_size
self.contents = {}
Our hash function is also very simple, and unlike a regular hash function, all it does is classify points into their surrounding cells. It takes a 2D point as its parameter, divides each element by the cell size, and casts it to an (int, int) tuple.
def _hash(self, point):
return int(point.x/self.cell_size), int(point.y/self.cell_size)
How does one insert objects?
There simplest keys to insert are single points. These aren't generally that useful, but the concept is straightforward, and they might be used for way-points, or similar. The procedure is extremely simple: hash the point to find the right bucket, create the bucket if it doesn't yet exist, and insert the object into the bucket. In this implementation, each bucket is a simple Python list.
def insert_object_for_point(self, point, object):
self.contents.setdefault( self._hash(point), [] ).append( object )
Of course, we also need to insert more complex shapes. Rather than deal with the intricacies of determining which bucket(s) an arbitrary shape need to hash to, we support only one other primitive: the axis-aligned bounding-box. The axis-aligned bounding-box is cheap to compute for other primitives, provides a reasonably decent fit, and is incredibly simple to hash.
The astute among you will have already noticed a few problems with inserting objects other than simple points into the spatial hash: a) the object may overlap several cells/buckets if it is near the edge of a bucket, and b) an object may actually be larger than a single bucket. The solution to these is luckily also simple: we add the object to all relevant buckets. And the bounding-box approach comes into its own, as we can just hash the min and max points, and then iterate over the affected buckets.
def insert_object_for_box(self, box, object):
# hash the minimum and maximum points
min, max = self._hash(box.min), self._hash(box.max)
# iterate over the rectangular region
for i in range(min[0], max[0]+1):
for j in range(min[1], max[1]+1):
# append to each intersecting cell
self.contents.setdefault( (i, j), [] ).append( object )
What about removing objects?
There are a number of approaches to removing objects from the hash, depending on your needs. The simplest (and the one I used in the accompanying code) is to use the key - feed the position/bounding-box back into the hash function, and remove the object from the resulting bucket(s).
If you don't know the key, you can always perform a linear search over the entire spatial hash, and remove the object wherever you find it, but this of course is not great from a performance standpoint.
And lastly, you can just clear the whole structure (by deleting all the buckets), and start fresh.
And search/retrieval?
Searching follows exactly the same procedure: feed the point into the hash function, and return the list of items in the bucket.
Of course, for this to be useful for collision detection, you also need to be able to search in a range, or in our case, a bounding-box. This once again follows the same idea as insertion and removal: hash the min and max of the bounding-box, iterate over the affected cells/buckets, and build a list of all objects encountered. There is one trick, however - this list is likely to contain (potentially a lot of) duplicates. We don't want the user to have to deal with duplicates, so you need to zap them in some way. The accompanying code does this by adding them to a set (which cannot by definition contain duplicates), and converting the set back to a list, but there are many possible approaches.
How do we tune the spatial hash?
Whenever hashed data structures are discussed, the question of tuning arises. In this sparse spatial hash, we only have a single parameter to tune, namely the cell size. This cell size can have a pronounced effect on performance - too large a cell size and too many objects will end up in the same cell, too small and objects will span too many cells.
As a (very approximate) rule of thumb, I find that the cell size should be roughly twice the size of the average-sized object in your world. However, depending on the relative scales of objects, you may need to tune differently.
What else affects performance?
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?

There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
def __init__(self, cell_size):
self.cell_size = cell_size
self.contents = {}
def _hash(self, point):
return int(point.x/self.cell_size), int(point.y/self.cell_size)
There simplest keys to insert are single points. These aren't generally that useful, but the concept is straightforward, and they might be used for way-points, or similar. The procedure is extremely simple: hash the point to find the right bucket, create the bucket if it doesn't yet exist, and insert the object into the bucket. In this implementation, each bucket is a simple Python list.
def insert_object_for_point(self, point, object):
self.contents.setdefault( self._hash(point), [] ).append( object )
Of course, we also need to insert more complex shapes. Rather than deal with the intricacies of determining which bucket(s) an arbitrary shape need to hash to, we support only one other primitive: the axis-aligned bounding-box. The axis-aligned bounding-box is cheap to compute for other primitives, provides a reasonably decent fit, and is incredibly simple to hash.
The astute among you will have already noticed a few problems with inserting objects other than simple points into the spatial hash: a) the object may overlap several cells/buckets if it is near the edge of a bucket, and b) an object may actually be larger than a single bucket. The solution to these is luckily also simple: we add the object to all relevant buckets. And the bounding-box approach comes into its own, as we can just hash the min and max points, and then iterate over the affected buckets.
def insert_object_for_box(self, box, object):
# hash the minimum and maximum points
min, max = self._hash(box.min), self._hash(box.max)
# iterate over the rectangular region
for i in range(min[0], max[0]+1):
for j in range(min[1], max[1]+1):
# append to each intersecting cell
self.contents.setdefault( (i, j), [] ).append( object )
What about removing objects?
There are a number of approaches to removing objects from the hash, depending on your needs. The simplest (and the one I used in the accompanying code) is to use the key - feed the position/bounding-box back into the hash function, and remove the object from the resulting bucket(s).
If you don't know the key, you can always perform a linear search over the entire spatial hash, and remove the object wherever you find it, but this of course is not great from a performance standpoint.
And lastly, you can just clear the whole structure (by deleting all the buckets), and start fresh.
And search/retrieval?
Searching follows exactly the same procedure: feed the point into the hash function, and return the list of items in the bucket.
Of course, for this to be useful for collision detection, you also need to be able to search in a range, or in our case, a bounding-box. This once again follows the same idea as insertion and removal: hash the min and max of the bounding-box, iterate over the affected cells/buckets, and build a list of all objects encountered. There is one trick, however - this list is likely to contain (potentially a lot of) duplicates. We don't want the user to have to deal with duplicates, so you need to zap them in some way. The accompanying code does this by adding them to a set (which cannot by definition contain duplicates), and converting the set back to a list, but there are many possible approaches.
How do we tune the spatial hash?
Whenever hashed data structures are discussed, the question of tuning arises. In this sparse spatial hash, we only have a single parameter to tune, namely the cell size. This cell size can have a pronounced effect on performance - too large a cell size and too many objects will end up in the same cell, too small and objects will span too many cells.
As a (very approximate) rule of thumb, I find that the cell size should be roughly twice the size of the average-sized object in your world. However, depending on the relative scales of objects, you may need to tune differently.
What else affects performance?
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?

There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
Searching follows exactly the same procedure: feed the point into the hash function, and return the list of items in the bucket.
Of course, for this to be useful for collision detection, you also need to be able to search in a range, or in our case, a bounding-box. This once again follows the same idea as insertion and removal: hash the min and max of the bounding-box, iterate over the affected cells/buckets, and build a list of all objects encountered. There is one trick, however - this list is likely to contain (potentially a lot of) duplicates. We don't want the user to have to deal with duplicates, so you need to zap them in some way. The accompanying code does this by adding them to a set (which cannot by definition contain duplicates), and converting the set back to a list, but there are many possible approaches.
How do we tune the spatial hash?
Whenever hashed data structures are discussed, the question of tuning arises. In this sparse spatial hash, we only have a single parameter to tune, namely the cell size. This cell size can have a pronounced effect on performance - too large a cell size and too many objects will end up in the same cell, too small and objects will span too many cells.
As a (very approximate) rule of thumb, I find that the cell size should be roughly twice the size of the average-sized object in your world. However, depending on the relative scales of objects, you may need to tune differently.
What else affects performance?
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?

There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
Apart from the cell size parameter, there are a number of issues that can affect your performance.
The first issue is the size (and density) of your game world. While spatial hashes perform admirably with many objects, they perform best if the objects are sparsely distributed. If you have a small game world, and objects are closely clustered around each other, a dynamic quad-tree might be a better approach.
The next issue is the performance of the underlying container implementation. If you recall, we use the results of our hash function (which are integer tuples) as keys into a Python dictionary (which is itself a hash map). You can substitute whatever container you like, but be aware that your performance is heavily dependent on the performance of this container.
Didn't you mention useful tricks?
Yes I did, but I also lied - I am afraid that I only have one useful trick for you today.
Today's useful trick is how to intersect a line segment with the spatial hash. If you think about this for a moment, the problem is actually how to intersect a line with a grid.
At this point I am going to go off on a short rant: Many of the blog posts/articles on the internet which deal with this topic use the brute force approach of repeated ray<->bounding-box intersections. This is inefficient, and generally unnecessary.
Now with that out of the way, let us go through the approach. We know we want to find the cells in a regular grid, which intersected by a line - remind you of anything yet? How about now?

There is our regular grid, there is our line, there are our intersected cells. Yup, line<->grid intersection is better known as line rasterisation. Now, if you did graphics programming back in the day, you will recall that there is an efficient method to rasterise lines, know as Bresenham's algorithm. I won't bore you with the details here - Wikipedia has a decent explanation (see further reading, below), and the attached source code contains an implementation.
As for using it to perform spatial hash look-ups, we rasterise the line onto the cell grid, and at each pixel of the line, we grab the matching bucket and return it, once again eliminating duplicates.
You may be thinking that Bresenham's algorithm does not guarantee to produce 100% coverage of the line, and you would be correct. However, the algorithm can at most miss a small fraction of one corner of a cell, which is generally good enough. If you absolutely need to ensure no misses, you can adapt the line rasterising to suit, or even take an approach along the lines of anti-aliasing.
Further reading
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm
Conclusion
I hope you come away from this with a decent understanding of what spatial hashing is, how it works, and what it can do for you. Please don't hesitate to provide me with comments, suggestions or corrections.
Tristam MacDonald - [http://swiftcoder.wordpress.com]
Entity Crisis: Spatial Hashing - http://entitycrisis....al-hashing.html
Spatial hashing implementation for fast 2D collisions - http://conkerjo.word...-2d-collisions/
Wikipedia: Bresenham's line algorithm - http://en.wikipedia...._line_algorithm






Hello there,
Thanks for the article :) I have my SpatialHashing implementation in place. What brought me here is that I need to create a method in my class that returns the buckets that intersect the line. In other words the rasterise algorithm. Do you know of anywhere that I can find some pseudocode or implementation for it?
Thanks!