To write a proper non pseudo RNG, use multi threading :D

google for “is chaos deterministic”. It says up front that chaos is deterministic.

Ok, so there’s classical chaos, and quantum chaos. Sound about right?

At any rate, I found a sweet Catmull-Rom implementation: https://github.com/chen0040/cpp-spline​

I used Catmull-Rom curves instead of Bezier curves, because Catmull-Rom curves are continuous where the Bezier curves are not.

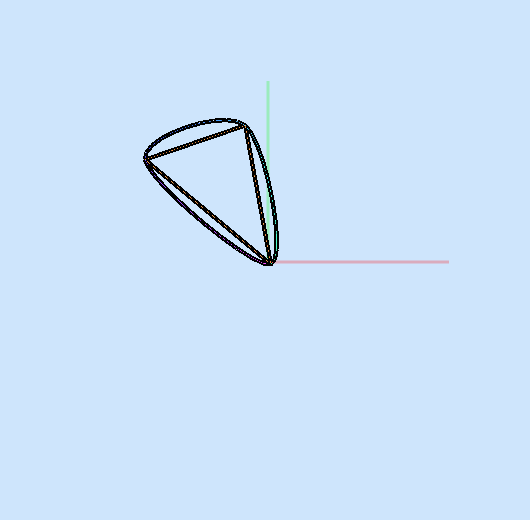
Ah, i see what you used the curves for.

taby said:
because Catmull-Rom curves are continuous where the Bezier curves are not.

To make bezier smooth, you can do something like this:

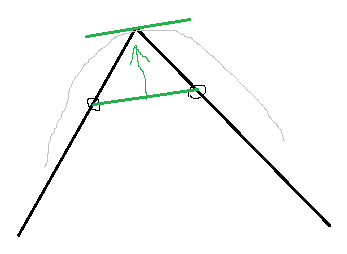
Take the positions at both line segments at  ⅓ of their length. (Or ½ for less sharp corners. The exact value we need to create a perfect circle from a square is somewhere in between.)

Take the (green) line between those points and transport it at its center to the ‘vertex control point’ where the two lines meet.
This gives you left and right ‘internal control points’ for the two line segments. The others you get from the other vertices and the further line segments connected to them in the same way. Here an example with a multi segment curve:

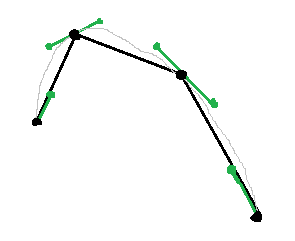
All the internal control point can be calculated automatically, and we get a result very similar to what you get from catmull rom using just the vertices. 

IIRC, if the left and right tangents of a green line have the same direction the curve is C1 continuous, if both their lengths are equal it's C2 continuous as well. (Both guaranteed from my proposal)

Postscript / Adobe tools support only such cubic bezier splines with 4 control points per segment. So all our fonts and logos are made this way. Artists often violate C2, but usually never C1 (aside of sharp corners ofc.).

So in practice i prefer bezier if i want to have manual control. But for procedural stuff where we just have some points, catmull rom is less complicated and easier to use, because there is no need to calculate nice internal points.

That's useful to know, maybe. I don't know the practical advantage of b-splines. Maybe this mostly shows with complex stuff like NURBS and its intersections.

Thanks for the info JoeJ.

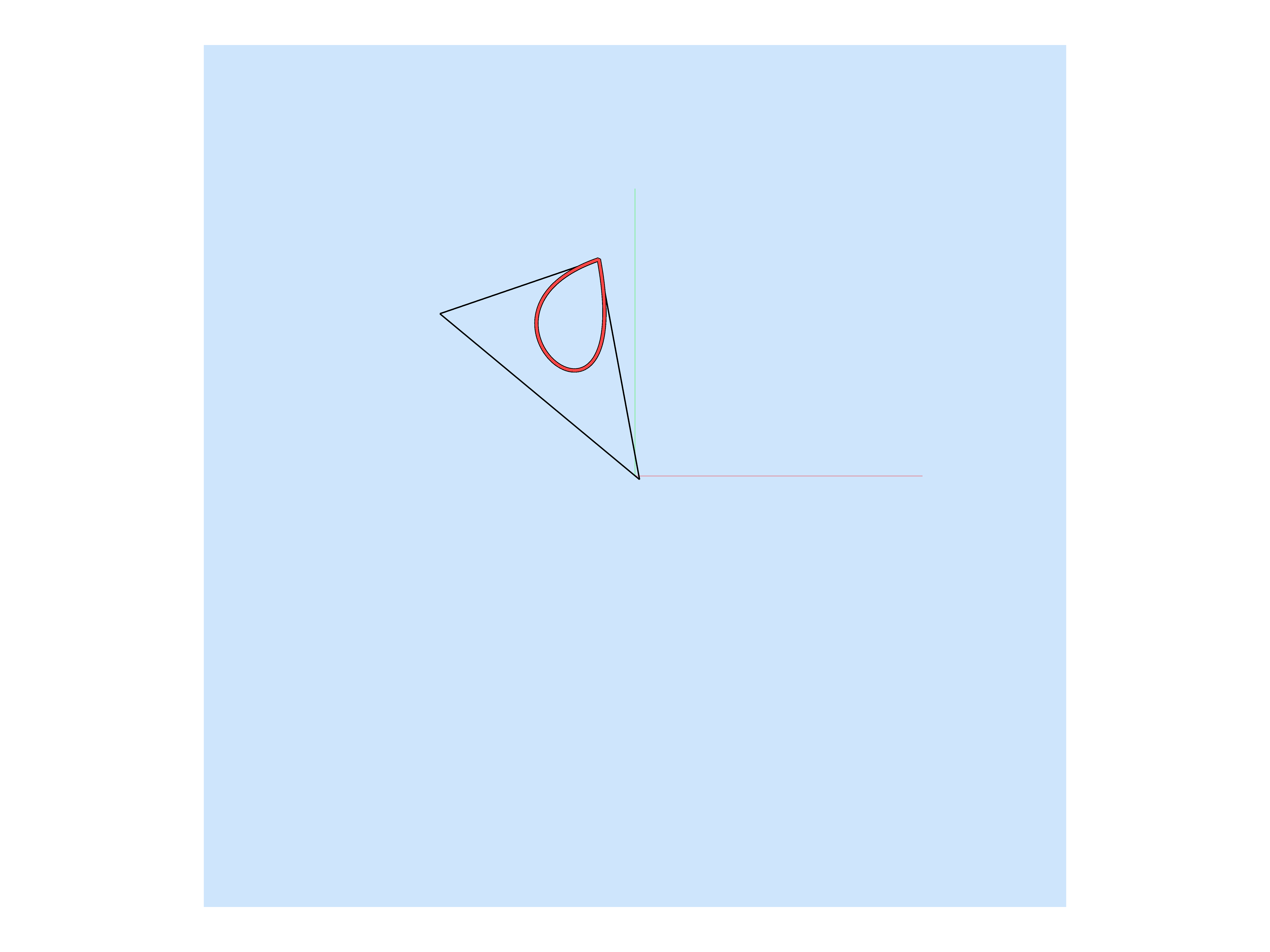
The library that I posted about supports all three types of curves: b-spline, Bezier, and Catmull-Rom. What I found was that for a triangle made up of 3 control points, the Bezier curve was discontinuous and does not necessarily run through the control points, the b-spline curve was continuous and inscribed by the triangle, and the Catmull-Rom curve is continuous and runs through the control points. Catmull-Rom is the perfect choice.

taby said:
What I found was that for a triangle made up of 3 control points, the Bezier curve was discontinuous and does not necessarily run through the control points

Yeah, but that's expected. Drawing in the ‘handles’ to ‘internal’ control points, like we would see in some DTP program…

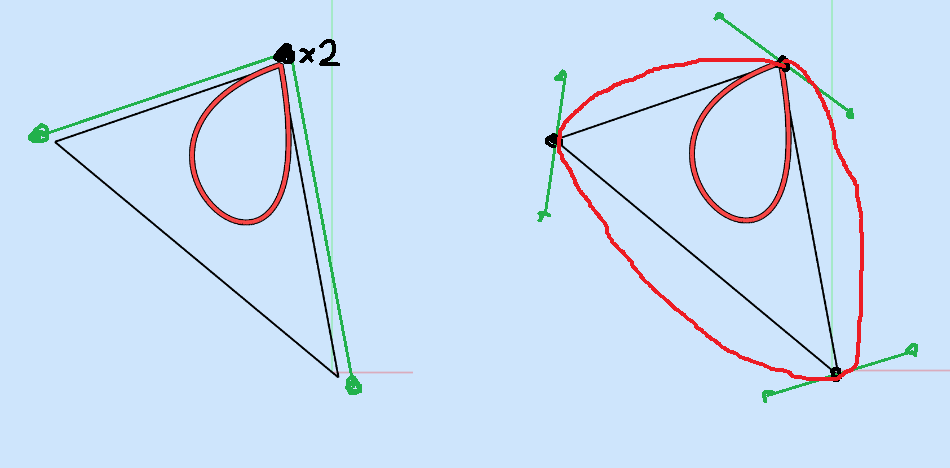
The left side is what you got maybe, the right side is what you wanted. Each edge of the triangle should be one cubic bezier segment with two CPs on vertices and two more ‘inside’. The vertex CPs can be shared with the next segment. So in total you would need 9 control points for the desired result.

But even if you did all the extrawork to make it work with bezier, result would be similar to catmull rom, which just works. 
Maybe you make a racing game sometime, then bezier would be more artist friendly to design a track.

taby said:
the b-spline curve was continuous and inscribed by the triangle, and the Catmull-Rom curve is continuous and runs through the control points.

… which inspires me to a better explanation:

With bezier, only the ‘vertex control points’ are on the curve, while the internal ‘handles’ give control over the tangent of the curve at those vertices.
So that's very different from the other two which seem more ‘simple’ from mathematical perspective, but bezier is very intuitive for manual design work.
From the programmers perspective, it's easier to replace the internal points with vectors originating from the vertex points imo.

You da man!

omg! I did just read fractals are real! https://www.quantamagazine.org/fractons-the-weirdest-matter-could-yield-quantum-clues-20210726/​

And they are not continuous. Thus our approaches to get smooth curves or distance functions are nothing but blasphemy! :D