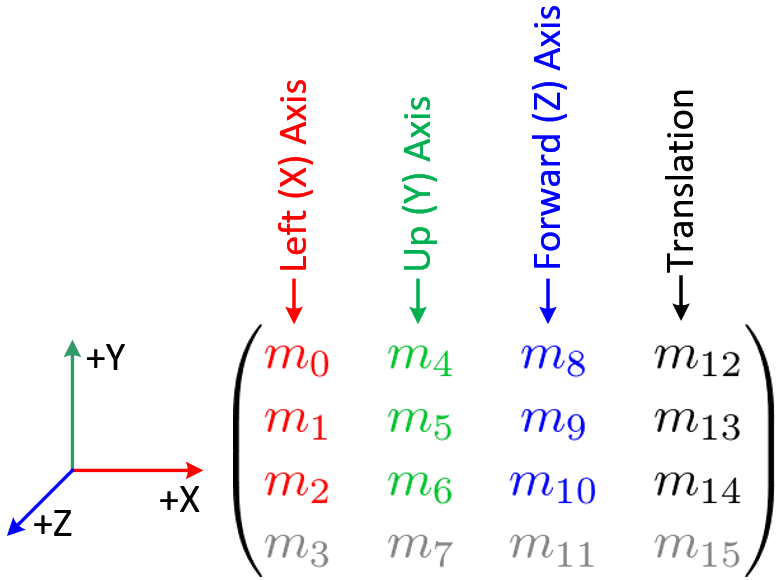
I'm trying to convert 3 direction vectors (forward, right, up vectors) to 3 Euler angles (X, Y, and Z).

I figured I could do this by projecting each axis against the unit axis, then use arctan2 to extract the angle.

Visualization:

I project the input right vector against the unit right (red) and unit up (green), then take the arctan2 of the resulting X,Y to get an angle. I do this for each axis respectively (see code snippet).

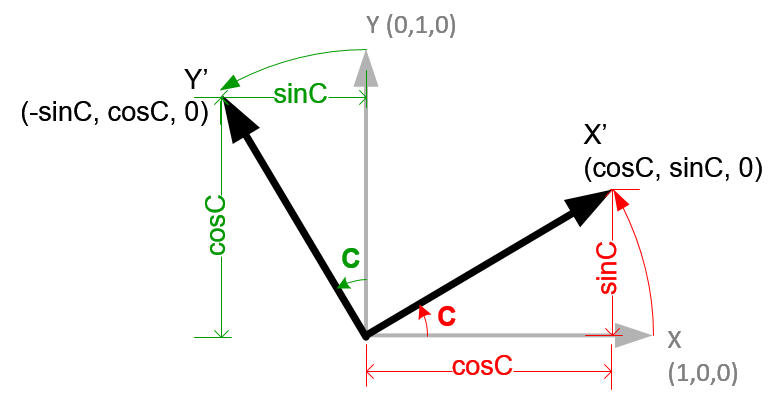
This generates the correct Euler rotation for an axis when the input axis vector is parallel to the "plane" its projected against. Once it starts deviating, the result becomes incorrect. Often times its close, but still not correct,

glm::vec3 rotation;

rotation.x = glm::degrees(atan2f(glm::dot(glm::vec3(0, 0, 1), up),
                                 glm::dot(glm::vec3(0, 1, 0), up)));


rotation.y = glm::degrees(atan2f(glm::dot(glm::vec3(1, 0, 0), forward),
                                 glm::dot(glm::vec3(0, 0, 1), forward)));


rotation.z = glm::degrees(atan2f(glm::dot(glm::vec3(0, 1, 0), right),
                                 glm::dot(glm::vec3(1, 0, 0), right)));

I'm using the glm math library if that makes a difference.

I don't know what "normalized axis angles" means. The usual representations are axis-angle, quaternion, rotation matrix and Euler angles. You can easily search the web for conversions between them.

Thanks for the reply. This link has a function (at the very bottom) for converting from Euler angles to a forward, right, and up vector. I'm trying to do the reverse. I've found lots of information on the web for quaternions and rotation matrices, but nothing related to the conversion I'd like to do.

As an aside, what are the forward, right, and up vectors usually refereed to as? Simply "direction vectors"?

I've found lots of information on the web for quaternions and rotation matrices, but nothing related to the conversion I'd like to do.

Using Bing, searching for "euler angles to quaternions" yields ~90,000 hits. Several of the first hits seem to be discussing what you describe.

I suspect that Alvaro's comment about your vectors results from your assumption that everyone will know what you mean, though you don't provide a context for the problem.

Using Bing, searching for "euler angles to quaternions" yields ~90,000 hits. Several of the first hits seem to be discussing what you describe.

Thanks for the reply, I get lots of hits for this too, but I'm not trying to convert to or from a quaternion. I'm trying to do the reverse of the anglesToAxes function as described here. e.g. 3 Vectors as input (a forward, right, and up vector) and 1 Vector output (the equivalent Euler angles). There are no quaternions at play here.

I did extract the vectors from a matrix like shown below:

Maybe I have some fundamental misunderstanding. The left, up, and forward vectors are not quaternions correct? They are just direction vectors (there is no W component).

I tried lots of things to get this to work, but everything has fallen short. For example, a suggestion I found (see 2nd post) described a technique using arccos, but arccos only returns angles for [0, pi]. I tried GLM's eulerAngles, but it doesn't always give correct results - sometimes the angle is wrong by as much as +/-10 degrees.

I'll gladly take any mockery for poor search skills so long as I can at least get a helpful link that actually provides a formula + explanation. When I do find something, all I seem to get are code dumps or half-baked explanations. I can't seem to find anything in-depth.