Introduction to XML Parametrization
In a video game's source code, there are many parameters and magic numbers . For instance, the maximum speed for a character running might be 20 km/h, their weapon shoots 1.5 bullets per second, and when they stop their speed drops by 60% per second.
A basic programming rule is to avoid using these 'magic' numbers directly in source code. Some of these numbers and parameters can be replaced with named constants, and some others are better located in configuration files (e.g. XML), out of the source code.
The advantages of taking the parameters out of the source code are well-known by video game programmers. These parametrization files can be changed without recompiling the source code, and in certain situations we can even change the parameter values and load them into the game at real-time, without a game restart.
One of the main points of parametrization files is that they can be configured by concept or level designers without any programming skills or access to source code changes. This is a must, for many of the game's parameters.
This article proposes an addition to this well-known design pattern, explaining a simple way to parametrize in XML the response curves that otherwise may be hard-coded.
Response Curves
Let's explain some response curve applications by example. The "moving and shooting" character example described earlier is in development, and the design team has updated the game specification document by adding some fresh great new features. Sound familiar?
Our example character - named Pepe, has a "stamina" bar ranged from 0 to 1 that measures how fatigued he is. The new feature is that Pepe reaches different maximum running speeds depending on his level of fatigue.
The response curve for this example will return the maximum running speed of Pepe for each stamina value. This curve can be very simple (a linear interpolation between the minimum and maximum speed possible), or very complex. For instance, we may want Pepe to run real fast when his stamina is higher than 0.8, slow between 0.8 and 0.4 and with very little speed difference between 0.4 and 0 (because we may find out that running too slow is not possible).
These game-play configurations are usually one of the designers responsibilities, and this article explains how to make these parameterizations easily configurable by the design team.
Implementation
One obvious option is to hard code this response curve, although it is the solution that this article avoids:
- Linear response curve: The maximum speed increases proportionally to the stamina bar. (fCurrentMaxSpeed = MAXSPEED * fStaminaBarValue)
- Quadratic response curve: When the stamina is lower, the max-speed changes slower than when the stamina is higher. (fCurrentMaxSpeed = MAXSPEED * fStaminaBarValue * fStaminaBarValue)
- More complex: It is a mix between the linear and quadratic, with a minimum speed of 0.2*MAXSPEED , but it could be whatever equation. (fCurrentMaxSpeed = MAXSPEED * ( 0.2 + ( fStaminaBarValue * fStaminaBarValue + fStaminaBarValue ) * 0.4f ))
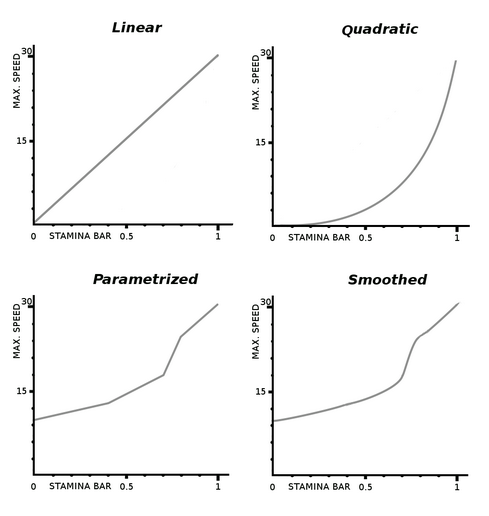 The proposed implementation for this kind of response curves is to configure them in a XML file out of the code. This solution provides much more flexibility to the response curve, making it easier to adapt its shape to the game needs.
The proposed implementation for this kind of response curves is to configure them in a XML file out of the code. This solution provides much more flexibility to the response curve, making it easier to adapt its shape to the game needs.
It is extremely more legible and easy to debug, understand and change, even by non-programmers.
The XML specifies the response curve, like so:
< Curve Name="Max speed per stamina" Input = " 0 0.4 0.7 0.8 1 " Output= " 10 12 18 25 30 " /> The game code contains the implementation of the object that keeps the XML loaded values and finds the result of the response curve for each given input. The ResponseCurve class has two public functions :- The constructor, that has as input parameters the data read from the XML, the curve name and the array of its inputs and outputs. (e.g. ResponseCurve (string curveName, float inputs[], float outputs[]) )
- The function that returns the output for each specific input. (float GetResult (float input) )
In our sample curve, GetResult(0.1) will return 10.5, meaning that with a stamina of 0.1 Pepe will have a maximum speed of 10.5 km/h. This function finds the two curve input values closest to the parameter input, and makes a linear interpolation between the two "output values".
It is possible to make a better interpolation than linear between the output points. We can use a spline algorithm (Catmull-Rom for instance) to get a smoothed response curve. It is less efficient than the linear interpolation, and in most cases it is difficult (or impossible) to see the difference in the game.
In most cases the linear interpolation is the best option.



