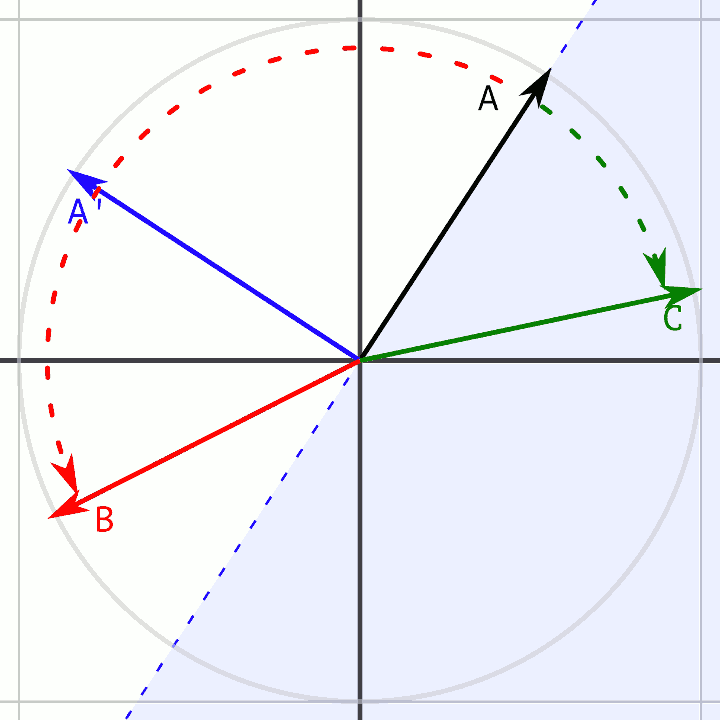
I am trying to rotate a vector to a goal vector.
My main problem now is that I can't wrap my head on is which way to rotate the vector, so finding the "shortest" way to rotate (clockwise or counter clockwise).

The dot product of the target vector and the normal of the current vector should result in a positive or negative value.  This result will determine whether a counter–clockwise or clockwise rotation should be made.

See attached.

Current direction vector A and its normal, A'
And sample target directions B and C:

Edit, its 2d, what I wrote was 3d.

If you use complex numbers to represent points and vectors, so you think of (x,y) as the number x+y*i, you can think of rotations as unit-length complex numbers, like cos(alpha)+sin(alpha)*i. Applying a rotation is now just complex-number multiplication. In that language, the rotation that maps a current vector to a target vector is simply z = target / current.

This might not be very satisfying because there is no notion of "shortest". The way mathematicians think of rotations, they are not things that happen progressively over time or anything like that, but just mappings that take an input vector and produce an output vector. 

If you want to recover a notion of "shortest", perhaps you are interested in limiting how much the current vector can change in one step. This code would do that:

Complex limited_rotation(Complex current, Complex target, Complex max_rotation) {
  Complex z = target / current;
  // You may want to normalize z here if you can't guarantee that current and target have the same length
  if (z.real() > max_rotation.real())
    return z;
  if (z.imag() > 0)
    return max_rotation;
  return conj(max_rotation);
}