Hey Dirk,
Could you please explain gauss map magic from your slides.First of all how to build gauss map?
Wikipedia says gauss map is mapping of polyhedron surface to the unit sphere.
I imagine this like some kind of projection to the unit sphere.But in this cases polyhedron face won't transform to any vertex(it will become sphere segment).
Separating axis theorem 3D - polygons
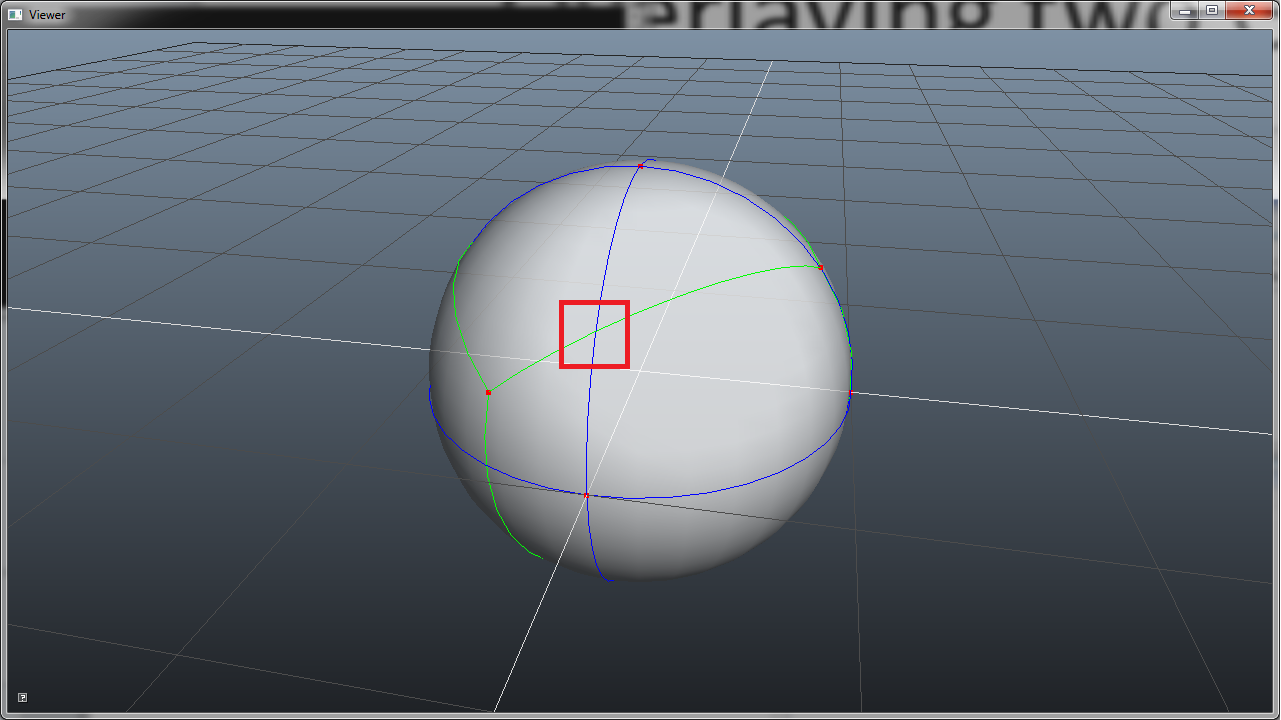
I think I cannot explain the Gauss-Map here any better than in the slides. The key points are (as pointed out in the presentation) that every face normal becomes a point on the unit sphere and every edge becomes an arc.
There is no need to build a Gauss-Map explicitely.The HE structure provides all information you need. For every edge you can find the two adjacent faces. The adjacent faces give you the vertices on the unit sphere and the arc between these two vertices corresponds to the edge you want to test…
I think I got it.
They key point is face normals.
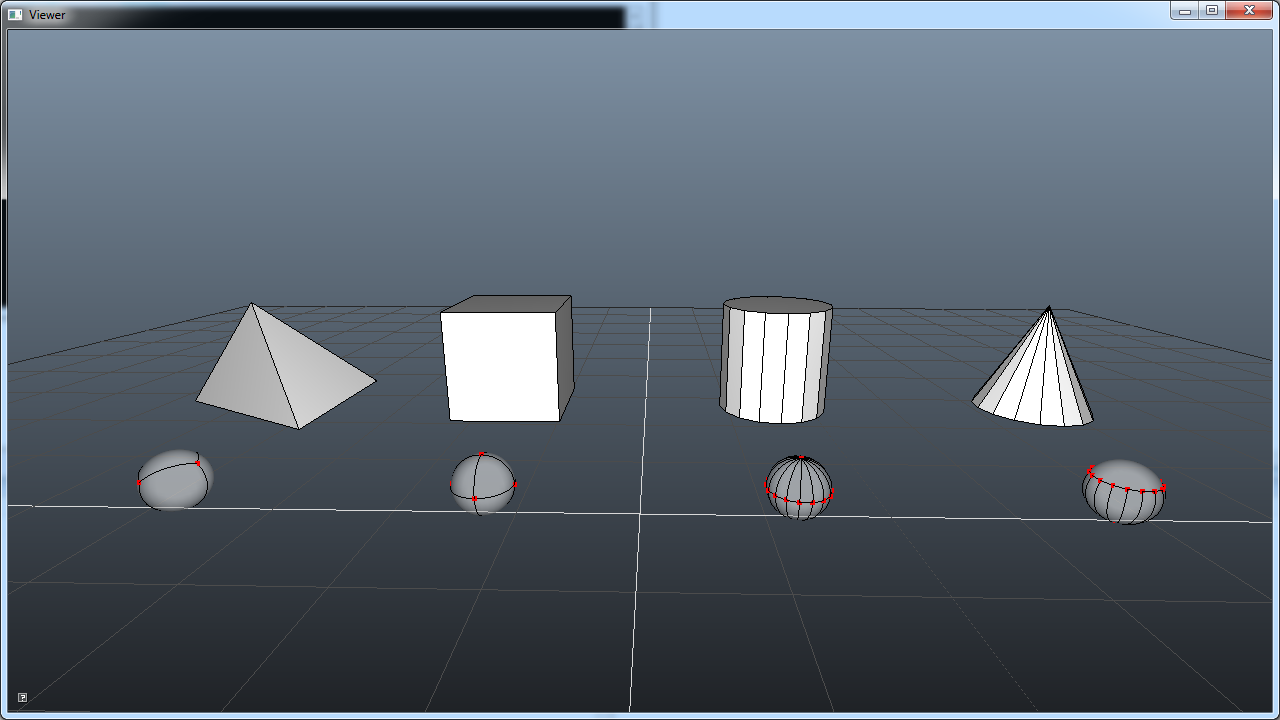
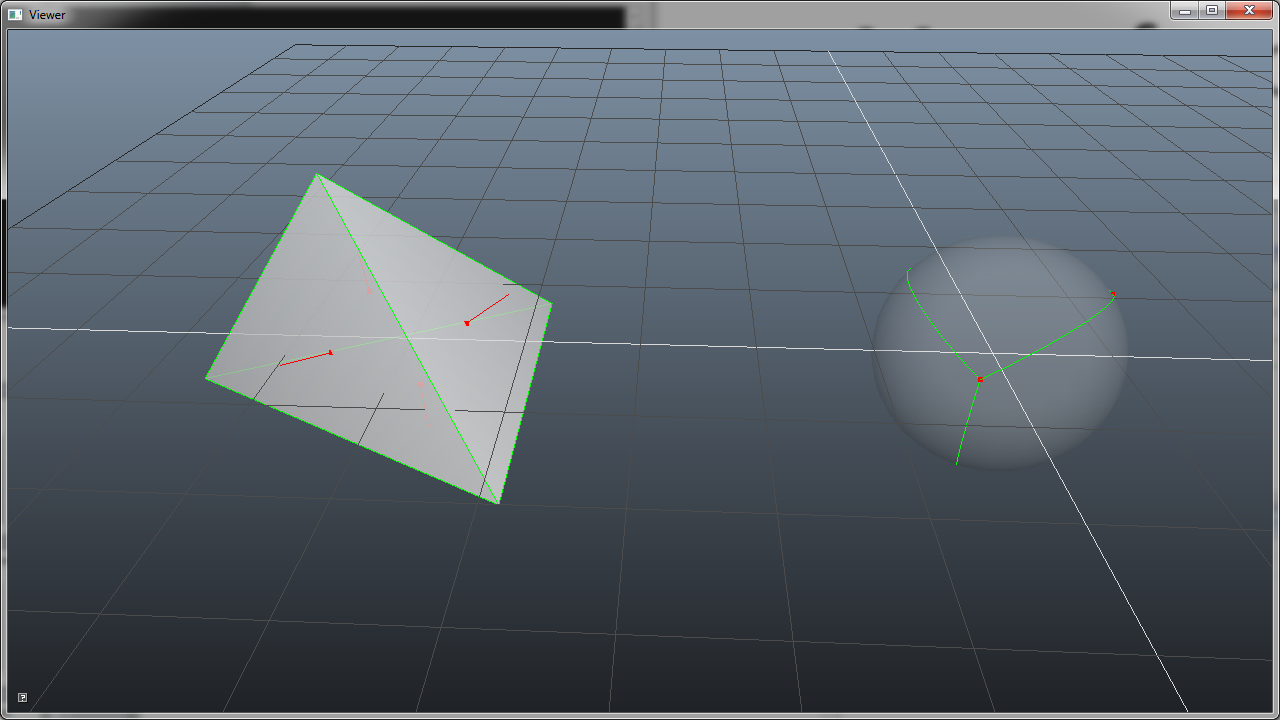
Shrink each face to a single oriented point(normal).After such deformation project everything to the unit sphere.
Here is how I think about this:
- For every face on the polytope, take its normal (unit length) and make it a point on the unit sphere
- For every edge on the polytope you have two associated faces. These faces each have a corresponding point on the unit sphere. Draw an arc on the surface of the unit sphere between these points
Now you can do this for two polytopes at the same time and by inspection you can make geometric conclusions. I would not think of this as deformation or projection. The challenge of the SAT implementation is that I look at a geometric problem from three different angles:
- A classic geometric view
- Minkowski space
- Gauss-Map
The trick is to combine these observations from each view and come to a single conclusion.
HTH,
-Dirk