Symbolic AI Systems vs Connectionism
Symbolic AI systems manipulate symbols, instead of numbers. Humans, as a matter of fact, reason symbolically (in the most general sense). Children must learn to speak before they are able to deal with numbers for example. More specifically, these systems operate under a set of rules, and their actions are determined by these rules. They always operate under task oriented environments, and are wholly unable to function in any other case. You can think of symbolic AI systems as "specialists". A program that plays 3d tic tac toe will not be able to play PenteAI (a game where 5 in a row is a win, but the players are allowed to capture two pieces if they are sandwiched by the pieces of an opposing player). Although symbolic AI systems can't draw connections between meanings or definitions and are very limited with respect to types of functionality, they are very convenient to use for tackling task-center problems (such as solving math problems, diagnosing medical patients etc.). The more flexible approach to AI involves neural networks, yet NN systems are usually so underdeveloped that we can't expect them to do "complex" things that symbolic AI systems can, such as playing chess. While NN systems can learn more flexibly, and draw links between meanings, our traditional symbolic AI systems will get the job done fast.
An example of a programming language designed to build symbolic AI systems is LISP. LISP was developed by John McCarthy during the 1950s to deal with symbolic differentiation and integration of algebraic expressions.
Production Systems
(This model of production systems is based on chapter 5 of Stan Franklin's book, The Artificial Mind, the example of the 8-puzzle was also based on Franklin's example)
Production systems are applied to problem solving programs that must perform a wide-range of seaches. Production ssytems are symbolic AI systems. The difference between these two terms is only one of semantics. A symbolic AI system may not be restricted to the very definition of production systems, but they can't be much different either.
Production systems are composed of three parts, a global database, production rules and a control structure.
The global database is the system's short-term memory. These are collections of facts that are to be analyzed. A part of the global database represents the current state of the system's environment. In a game of chess, the current state could represent all the positions of the pieces for example.
Production rules (or simply productions) are conditional if-then branches. In a production system whenever a or condition in the system is satisfied, the system is allowed to execute or perform a specific action which may be specified under that rule. If the rule is not fufilled, it may perform another action. This can be simply paraphrased:
| A Production System Algorithm
|
For a scenerio where a production system is attempting to solve a puzzle, pattern matching is required to tell whether or not a condition is satisfied. If the current state of a puzzle matches the desired state (the solution to the puzzle), then the puzzle is solved. However, if this case is not so, the system must attempt an action that will contribute to manipulating the global database, under the production rules in such a way that the puzzle will eventually be solved.
 |  |
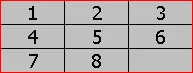
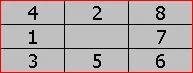
| Initial State | Final State |
In order to take a closer look to control structures let us look at a problem involving the eight puzzle. The eight puzzle contains eight numbered squares laid in a three-by-three grid, leaving one square empty. Initially it appears in some, obfuscated state. The goal of the production system is to reach some final state (the goal). This can be obtained by successively moving squares into the empty position. This system changes with every move of the square, thus, the global database changes with time. The current state of the system is given as the position and enumeration of the squares. This can be represented for example as a 9 dimensional vector with components 0, 1, 2, 3,..., 8, NULL, the NULL object being the empty space.
In this puzzle, the most general production rule can be simply summed up in one sentence:
If the empty square isn't next to the left edge of the board, move it to the left
However, in order to move the empty square to the left, the system must first make room for the square to move left. For example, from the initial state (refer to above figure) the 1-square would be moved down 1 space, then, the 8-square right 1 space, then the 6-square up one space in order for the empty square to be moved left (i.e., a heuristic search). All these sequences require further production rules. The control system decides which production rules to use, and in what sequence. To reiterate, in order to move the empty square left, the system must check if the square is towards the top, or somewhere in the middle or bottom before it can decide what squares can be moved to where. The control system thus picks the production rule to be used next in a production system algorithm (refer to the production system algorithm figure above).
Another example of a production system can be found in Ed Kao's 3-dimensional tic-tac-toe program. The rules and conditions for the AI are conviently listed just like for the 8 puzzle.
The question that faces many artificial intelligence researchers is how capable is a production system? What activities can a production system control? Is a production system really capable of intelligence? What can it compute? The answer lies in Turing machines...
Programs
These programs written are examples of production systems.
- 3d Tic Tac Toe - E. Kao
- PenteAI - J. Matthews